WHAT

• A study to probe deeper into the relationship between mathematical aspects of a problem and the modifications needed so that it can be investigated/ solved on a computer in an upper-level undergraduate math problem-solving course.
• The aim is to inform teaching practice, for instance by identifying situations where students experience difficulties, and by exposing misconceptions in their thinking and approaches.
• The study will attempt to identify “good” math problems of two kind: problems that help students learn basic programming skills, and those that naturally invite investigations using programming.

WHO

• Miroslav Lovric, McMaster University

Collaborators

• Chantal Buteau, Brock University
• Ami Mamolo, UOIT
• Erin Clements, Ph.D. Candidate, Western University.

 

WHEN

• 2015-2018

OUTCOMES

• A better understanding of a mathematician’s perceptions and awarenesses related to incorporating problem-based activities requiring computational thinking into an upper-level undergraduate mathematics course. Data from the case study is qualitative in nature and seeks to present an in-depth account of one professor’s experiences developing and teaching computational thinking in and for mathematics.  Analyses highlight the similarities and differences amongst the values and opportunities perceived for computational thinking versus other more ubiquitous mathematical approaches, as well as the perceived tensions and challenges in trying to foster such values and opportunities.
• Understanding that there is no unique, best way to teach programming, both as a skill and as a tool used for problem-solving in mathematics. For instance, while some students agree that a hands-on experience worked best for them, one student says that “Maybe a bit of lecturing could be done to teach the basics.” This is particularly relevant for programs where, due to a large size (150+ students) and instructor’s own preferences, programming is taught by lecturing and demonstrating (i.e., no active involvement from students).
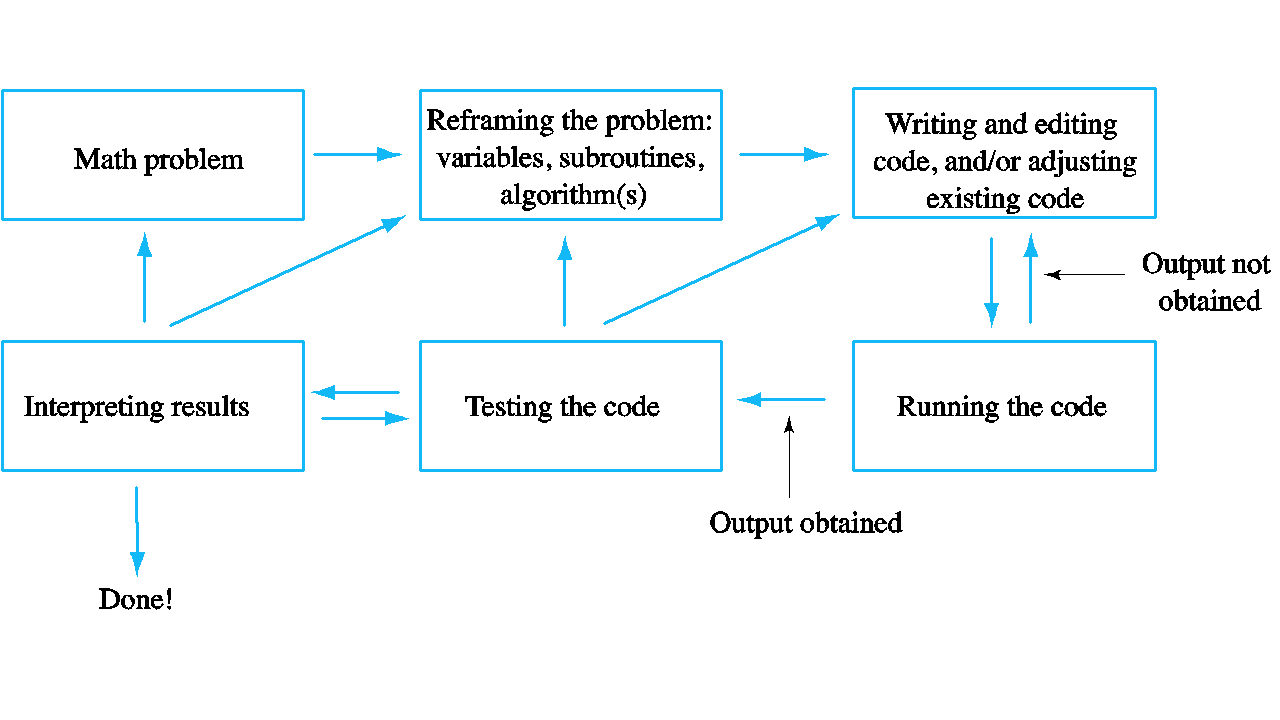
• Pedagogical situations that surfaced in teaching a problem-solving course in mathematics with computer programming were analyzed. To frame the narratives and facilitate the analysis, a mathematics programming model was built, which in many ways parallels the model that is employed in working with applications in mathematics. Misconceptions and challenges that students face in programming were investigated, for instance when they code nested conditional statements and loops and navigate between multiple meanings of the equals sign. Mathematics concepts, such as the difference between a true value of a number and its approximations, or the meaning and purpose of a variable, come to the foreground when students engage with programming tasks.

 

DISSEMINATION

• Lovric, M. & Mamolo, A (2017). Computational Thinking in and for Undergraduate Mathematics: Perspectives of a Mathematician.  20^th Annual Conference on RUME Proceedings. San Diego.
• Lovric, M. (Submitted). Programming and Mathematics in an Upper-Level University Problem-Solving Course. PRIMUS.

 

NEXT STEPS

• Focus on the analysis of collected data.
• Produce 2 detailed lesson plans of using computational thinking in mathematics education at a tertiary level, along with necessary resource and support material The purpose will be to test some of the findings.
• Produce a 5-10 minute video interview to document the research.